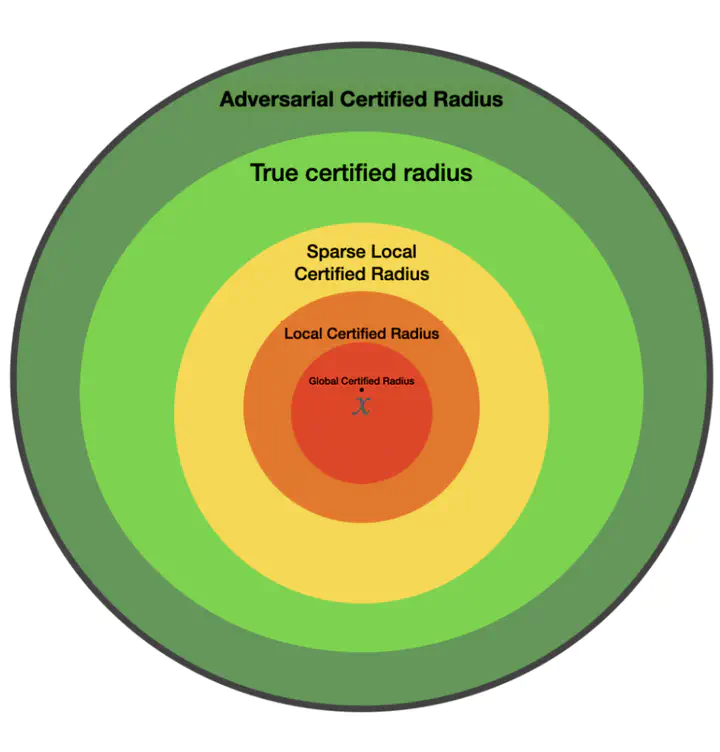
 Hierarchy of Certified Robustness
Hierarchy of Certified RobustnessAbstract
This work studies the adversarial robustness of parametric functions composed of a linear predictor and a non-linear representation map. Our analysis relies on sparse local Lipschitzness (SLL), an extension of local Lipschitz continuity that better captures the stability and reduced effective dimensionality of predictors upon local perturbations. SLL functions preserve a certain degree of structure, given by the sparsity pattern in the representation map, and include several popular hypothesis classes, such as piece-wise linear models, Lasso and its variants, and deep feed-forward ReLU networks. We provide a tighter robustness certificate on the minimal energy of an adversarial example, as well as tighter data-dependent non-uniform bounds on the robust generalization error of these predictors. We instantiate these results for the case of deep neural networks and provide numerical evidence that supports our results, shedding new insights into natural regularization strategies to increase the robustness of these models.